Principle Component Analysis in Python

While there a number of tutorials and pages better devoted to the subject of principle component analysis (PCA), this post is geared towards providing a simple example of this data classification method in python. Much of the algorithm code was provided by Henning Risvik. This module along with numpy, scipy, and matplotlib are required for this example to function. The data used for this example are derived from the physical properties of the planets (the debate over Pluto's status is for another post but is assumed to retain it's planet privileges for this post). The pca module required for this example can be found here.

'''
PCA example using python.  Very simplified
'''

import pca_module as pca
import numpy as N
import pylab as P
'''
Adapted from:

http://www.cs.mcgill.ca/~sqrt/dimr/dimreduction.html

[title]  Planets of the Solar System
[source] http://pds.jpl.nasa.gov/planets/

[columns]  distance  diameter  density
"Mercury"    0.387     4878     5.42   (black)
"Venus"      0.723    12104     5.25   (black)
"Earth"      1.000    12756     5.52   (black)
"Mars"       1.524     6787     3.94   (black)
"Jupiter"    5.203   142800     1.314  (blue)
"Saturn"     9.539   120660     0.69   (blue)
"Uranus"    19.18     51118     1.29   (blue)
"Neptune"   30.06     49528     1.64   (blue)
"Pluto"     39.53      2300     2.03   (blue)

'''
RawPlanets = N.array([
              [0.39,4878,5.42],
              [0.72,12104,5.25],
              [1,12756,5.52],
              [1.52,6787,3.94],
              [5.2,142800,1.31],
              [9.54,120660,0.69],
              [19.18,51118,1.29],
              [30.06,49528,1.64],
              [39.53,2300,2.03]])

#Normalize the raw values
dataMatrix = N.log10(RawPlanets)

#perform PCA--thanks Henning Risvik
scores,  loading,  explanation = pca.PCA_nipals2(dataMatrix, standardize=True)

pc1 = scores[:, 0]
pc2 = scores[:, 1]
pc3 = scores[:, 2]

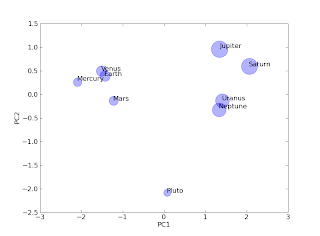
fig=P.figure()#create pylab figure
ax = fig.add_subplot(111)#create an ax

#add scatter plot and size based upon distance from sun
ax.scatter(pc1, pc2, color = 'b', s = dataMatrix[:,1]**4, alpha = 0.3)

#add axis labels
ax.set_xlabel('PC1', fontsize = 12)
ax.set_ylabel('PC2', fontsize = 12)

#data labels
labels = ['Mercury','Venus', 'Earth', 'Mars', 'Jupiter', 'Saturn', 'Uranus', 'Neptune', 'Pluto']
#add labels to each marker
for label, x, y in map(None, labels, pc1, pc2):
    ax.annotate(label, xy=(x, y),  size = 12)

P.show()

Slow Mo Bubble Burst

This is an amazing video detailing the slow motion video capture of a bubble bursting. While it does not seem like much, it can be terribly fascinating. Fast forward to just under 4:00 for the slow motion capture.

Fitting an Arbitrary Function in Python

While peak areas may be measured directly through trapezoidal integration, in some cases the true analytical signal is convoluted with some degree of noise (whether that noise is stochastic or systematic is another matter). One solution minimize the contribution of noise to a particular signal is through fitting. While fitting a least squares line can be easily achieved using a simple scientific calculator, the fitting of more complex functions is, you guessed it, more complex. Not only is the function itself more involved than a straight line, the fitting methods used often require a initial fitting parameters to start. Often these are educated guesses regarding the nature of the data you are trying to fit. Below is an example of fitting both a gaussian and exponentially modified gaussian functions (common chromatographic peak shapes) to hypothetical data. Perhaps the two most salient features in the code snippet below are the use of the FFT to convolute two different functions to create the EMG and the use of a fairly generic syntax which accepts a variable number of parameters and an arbitrary function to fit the data. This code snippet was highly influence by the information already posted on the scipy website regarding function fitting.

The next task...how to tell the difference between the fitted function and the actual data? Any takers?

I should also note that another good example can be found here.

import numpy as N
import numpy.fft.fftpack as F
'''

Next how to calculate area?
'''

def expGauss(x, pos, wid, tConst, expMod = 0.5, amp = 1):
'''
x -- numpy array
pos -- centroid position
wid -- width
tConst -- time constance for exponential decay
amp -- amplitude of peak
expMod -- modifies the amplitude of the peak -- must be a float

Forumulas used:

y = a * exp(-0.5 * (x-b)^2 / c^2) --traditional gaussian forumla
exp = N.exp(-1*expMod*N.arange(0,len(y))/Const) --function that is merged with the gaussian

Note if expMod is too small (i.e. goes towards zero) the function will return a flat line.
'''
expMod *=1.0
gNorm = amp * N.exp(-0.5*((x-pos)/(wid))**2)
g = expBroaden(gNorm, tConst, expMod)
return g, gNorm

def expBroaden(y, t, expMod):
fy = F.fft(y)
a = N.exp(-1*expMod*N.arange(0,len(y))/t)
fa = F.fft(a)
fy1 = fy*fa
yb = (F.ifft(fy1).real)/N.sum(a)
return yb

if __name__ == '__main__':
import scipy as S
import pylab as P
import scipy.optimize as optimize

a = N.arange(0,100,0.1)

tConstArray = N.arange(10,200,10)
x, x1 = expGauss(a, 50, 2, 150, 2, 5)
xN = x + 0.5-S.rand(len(a))/2
x1N = x1 + 0.5-S.rand(len(a))/2


# Fit the first set
#p[0] -- amplitude, p[1] -- position, p[2] -- width
fitfuncG = lambda p, x: p[0]*N.exp(-0.5*(x-p[1])**2/p[2]**2) # Target function
errfuncG = lambda p, x, y: fitfuncG(p, x) - y # Distance to the target function
p0 = [5.0, 50.0, 2.0] # Initial guess for the parameters
p1, success = optimize.leastsq(errfuncG, p0[:], args=(a, x1N))
p1G = fitfuncG(p1,a)

P.plot(x1N,  'ro', alpha = 0.4, label = "Gaussian")
P.plot(p1G, label = 'G-Fit')

'def expGauss(x, pos, wid, tConst, expMod = 0.5, amp = 1):'
#p[0] -- amplitude, p[1] -- position, p[2] -- width, p[3]--tConst, p[4] -- expMod
fitfuncExpG = lambda p, x: expGauss(x, p[1], p[2], p[3], p[4], p[0])[0]
errfuncExpG = lambda p, x, y: fitfuncExpG(p, x) - y # Distance to the target function
p0a = [3.5, 45., 3., 70., 2.] # Initial guess for the parameters
p1a, success = optimize.leastsq(errfuncExpG, p0a[:], args=(a, xN))
p1aG = fitfuncExpG(p1a,a)

print type(xN), type(a), len(xN), len(a)
P.plot(xN,  'go', alpha = 0.4, label = "ExpGaussian")
P.plot(p1aG, label = 'ExpG-Fit')

P.legend()
P.show()

Derivative in Python/Numpy

Though I don't use it very often, the following little snippet for python/numpy can be useful for the determination of an array's derivative. The image shows the use of this function to determine the derivative of a particular array to aid in a classical peak picking scheme using zero-crossings. Oddly enough there doesn't seem to be an explicit function to do this in scipy and/or numpy--or at least not that I'm aware. If anyone has a better solution please share.

def derivative(y_data):
'''calculates the 1st derivative'''
  y = (y_data[1:]-y_data[:-1])
  dy = y/2 #scaling factor that is not necessary but useful for my application
  #one more value is added because the length
  # of y and dy are 1 less than y_data
  return N.append(dy,dy.mean())

TopHat Filter

I'm always on the lookout for new methods for signal processing, especially related to mass spectrometry and general noise reduction. The tophat filter is a method borrowed from the image processing community that treats a 1D graph as a 2D black and white image. It is primarily used to remove the baseline noise that may be contained in a spectrum. This can be especially important for MALDI spectra that have a high background. An example of this processing may be found in the following document which also contains a number sample figures: Beating the Noise: New Statistical Methods for Detecting Signals in MALDI-TOF Spectra below Noise Level by Tim O.F. Conrad at the Free University of Berlin (pdf). The authors of this pdf are also connected with the OpenMS/TOPP project for proteomics data processing. I've also included a small script that I put together that will perform this function in python.

import numpy as N
from scipy import ndimage#used for tophat filter

def topHat(data, factor):
'''
data -- numpy array
pntFactor determines how finely the filter is applied to data.
A point factor of 0.01 is appropriate for the tophat filter of Bruker MALDI mass spectra.
A smaller number is faster but a trade-off is imposed
'''
pntFactor = factor
struct_pts = int(round(data.size*pntFactor))
str_el = N.repeat([1], struct_pts)
tFil = ndimage.white_tophat(data, None, str_el)

return tFil

File Dialogs in PyQt4

The following code is an example of how to setup a simple open file dialog prompt. Two versions are shown using the following code, the open file dialog and the open directory dialog. More examples may be found in the PyQt4 source code examples and also from the great general tutorial found at zetcode.

#!/usr/bin/python

from PyQt4 import QtCore, QtGui
import os

class OFD_Class(QtGui.QWidget):
       def __init__(self, parent = None):
           QtGui.QWidget.__init__(self, parent)
           self.curDir = os.getcwd()
          
       def PyQt4_OFD(self):
           directory= QtGui.QFileDialog.getExistingDirectory(self, "Select Folder",  self.curDir)
           if directory:
               #if user selected a directory...do something
               print directory
               #remember that PyQt returns QStrings which are unicode object and need to be handled appropriately
               print type(directory)
      
           dataFileName = QtGui.QFileDialog.getOpenFileName(self,\
                                                                    "Select File",\
                                                                    self.curDir, 'X!Tandem XML (*.xml);; HDF5 File (*.h5);;SQLite Database (*.db);;All Files (*.*)')
           if dataFileName:
               #if file selected...do something
               print dataFileName
               print type(dataFileName)

def main():

   import sys
   app = QtGui.QApplication(sys.argv)

   OFD = OFD_Class()
   OFD.PyQt4_OFD()

   sys.exit(app.exec_())

  

if __name__ == "__main__":
   main()

What is a Mach disk you ask?

high-speed-imaging-of-shock-waves-fig-13
Originally uploaded by clowersb

This is fantastic image which illustrates the wide range of gas dynamics that occur during a rapid expansion of a gas. In this particular image the Mach disk is visible as a vertical line located just to the right of center. From the perspective of fluid dynamics, after the Mach disk the behavior of a gas can become highly turbulent (observed as the swirling formations in the image). Also of interest is the relative speed and temperature of the particles immediately preceding and following the Mach disk. Prior to the Mach disk, the Mach number of the system ais much greater than 1 and subsonic following the disk. With respect to temperature, the region following the Mach disk is characterized by a rapid increase in temperature.

http://en.wikipedia.org/wiki/Shock_diamond